Construction of Perron Frobenius Operator from Computational Fluid Dynamics (CFD) Data
ABSTRACT
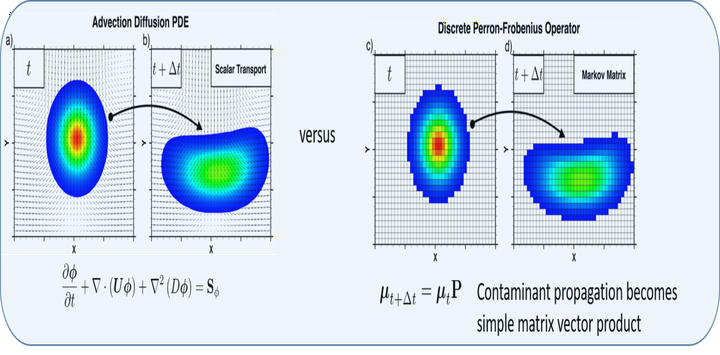
To model the contaminant transport consider the following advection-diffusion partial differential equation (PDE) with source term and output measurement.
\begin{align} & \frac{\partial \Phi}{\partial t} + \nabla( \bf{U}\Phi) +\nabla^2( \mathcal{D}\Phi) = S_{\Phi} \\ & y=\chi_{A_k}(\textbf{x})\Phi, \quad k=1,\ldots,p \label{Eq:1}\tag{1} \end{align}
where $\Phi(\textbf{x},t)$ is the scalar contaminant density at time $t$, $\textbf{x} \in X\subset{R}^n$ is the physical space, $\mathcal{D}$ is the diffusion constant and $S_{\Phi}$ is the source term in Eq.(\ref{Eq:1}). The contaminant is propagated by the $\bf U$ field which can be steady or can be a function of time. Flow field ($\bf U$) can be computed numerically using CFD or can be generated experimentally. $\chi_{A_k}(\textbf{x})$ for $k=1,\ldots,p$ denotes the indicator function for set $A_k\subset X$ and corresponds to the location of $p$ sensors. It is important to note that the advection-diffusion PDE Eq.(\ref{Eq:1}) describe linear evolution for the propagation of contaminant $\Phi$. This continuous time linear PDE evolution model can be replaced by its discrete-time equivalent by using the linear transfer P-F operator. In the absence of source term in Eq.(\ref{Eq:1}), the discrete-time evolution of advection-diffusion PDE is described by following P-F operator;
\begin{align} [ \mathbb{P} \mu] (A)=\int_X p(\textbf{x},A)d\mu(\textbf{x}) \end{align}
where $\mu\in {\cal M}(X)$ the space of real-valued measure and $p(\textbf{x},A)$ is stochastic transition function and describes the transition probability from point $\textbf{x}$ to set $A\subset X$. To compute the finite dimensional approximation of the P-F operator we only need the information about the nonlinear flow field $\bf U$ and the diffusion coefficient $\mathcal{D}$ as is described in the following section. An example of this is shown in above figure, where the velocity field is shown by vectors and the color contours as the initial concentration.